DiffuSeq: 확산 모델을 활용한 시퀀스-투-시퀀스 텍스트 생성의 혁신

DiffuSeq: 확산 모델을 활용한 시퀀스-투-시퀀스 텍스트 생성의 기술적 분석

확산 모델(Diffusion Model)은 최근 이미지와 오디오 생성에서 뛰어난 성과를 보이며 생성 AI의 중요한 패러다임으로 자리 잡았습니다. 그러나 이산적(discrete) 특성을 가진 텍스트 도메인, 특히 조건부 생성 문제에 이 모델을 적용하는 것은 여전히 도전 과제였습니다. 2023년 ICLR에 발표된 논문 “DiffuSeq: Sequence to Sequence Text Generation with Diffusion Models”은 이 문제를 해결하기 위한, 직관적이면서도 수학적으로 엄밀한 접근법을 제시합니다. 아래에서는 기본 개념부터 복잡한 메커니즘까지 단계별로 설명하겠습니다.

1. 확산 모델의 기본 개념

확산 모델은 크게 두 가지 과정으로 구성됩니다:

전방 과정(Forward Process)

• 정의: 원본 데이터에 점진적으로 노이즈를 추가하는 과정
• 목적: 충분한 시간이 지나면 원본 데이터가 완전한 노이즈로 변환됨

역방향 과정(Reverse Process)

• 정의: 노이즈로부터 원본 데이터를 점진적으로 복원하는 과정
• 목적: 생성 모델이 학습해야 할 부분으로, 노이즈에서 실제 데이터로의 변환을 학습

2. 수학적 정의와 표기법 설명

기본 표기법

• \(z_0\) : 원본 데이터의 연속적 표현 (확산 모델이 작동하는 연속 공간에서의 데이터)
• \(z_t\) : 시간 단계 \(t\) 에서의 노이즈가 추가된 데이터 (\(t\) 가 클수록 노이즈가 많이 포함됨)
• \(T\) : 총 확산 단계 수 (논문에서는 2,000 사용)
• \(q(z)\) : 실제 데이터 분포
• \(p_\theta(z)\) : 모델이 학습하려는 데이터 분포

전방 과정의 수학적 정의

원본 데이터 \(z_0 \sim q(z)\) 에 대해, 각 단계 \(t \in [1, 2, ..., T]\) 에서:

\[q(z_t|z_{t-1}) = \mathcal{N}(z_t;\sqrt{1 - \beta_t}z_{t-1}, \beta_tI)\]

여기서:

• \(\mathcal{N}(\mu, \sigma^2)\) : 평균 \(\mu\) , 분산 \(\sigma^2\) 을 가진 정규 분포
• \(\beta_t \in (0, 1)\) : 시간 \(t\)에서의 노이즈 크기를 결정하는 파라미터
• \(I\) : 단위 행렬 (노이즈가 각 차원에 독립적으로 추가됨을 의미)

역방향 과정의 수학적 정의

완전한 노이즈 \(z_T\) 에서 시작하여 원본 데이터를 복원:

\[p_\theta(z_{0:T}) := p(z_T)\prod_{t=1}^{T} p_\theta(z_{t-1}|z_t)\]

각 단계의 조건부 확률은 학습 가능한 파라미터 \(\theta\) 로 모델링됩니다:

\[p_\theta(z_{t-1}|z_t) = \mathcal{N}(z_{t-1}; \mu_\theta(z_t, t), \sigma_\theta(z_t, t))\]

여기서:

• \(\mu_\theta(z_t, t)\): 모델이 예측한 평균
• \(\sigma_\theta(z_t, t)\): 모델이 예측한 표준 편차

3. DiffuSeq 모델의 핵심 구성 요소

3.1 문제 정의와 표기법

DiffuSeq는 시퀀스-투-시퀀스(Seq2Seq) 텍스트 생성 작업을 수행합니다:

• \(w^x = \{w_1^x, ..., w_m^x\}\) : 길이 \(m\) 의 소스(입력) 시퀀스
• \(w^y = \{w_1^y, ..., w_n^y\}\) : 길이 \(n\) 의 타겟(출력) 시퀀스
• 목표: 주어진 \(w^x\) 에 대해 적절한 \(w^y\) 를 생성하는 확산 모델 학습

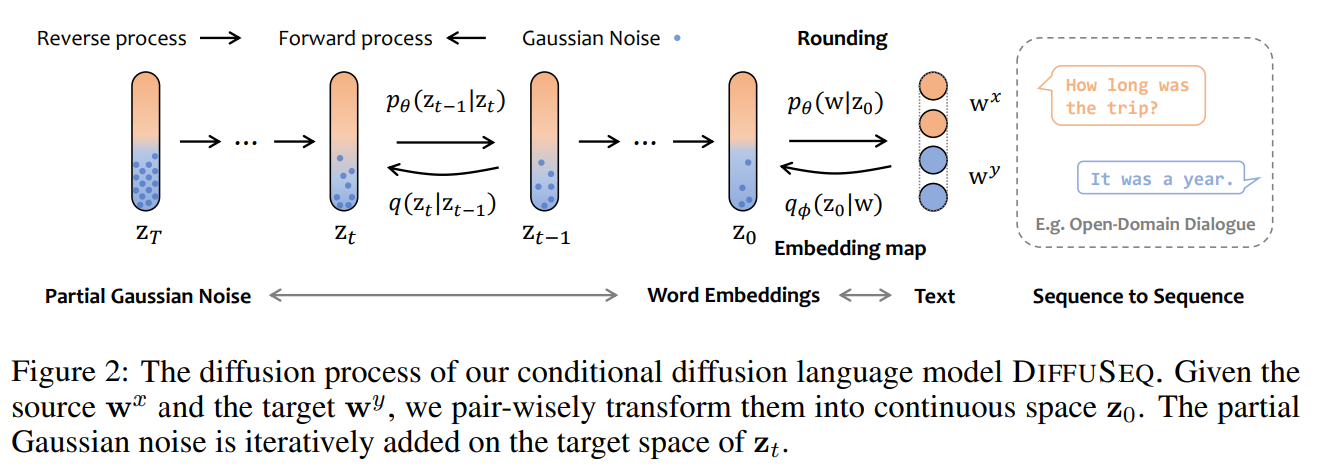
3.2 부분 노이징(Partial Noising) 메커니즘

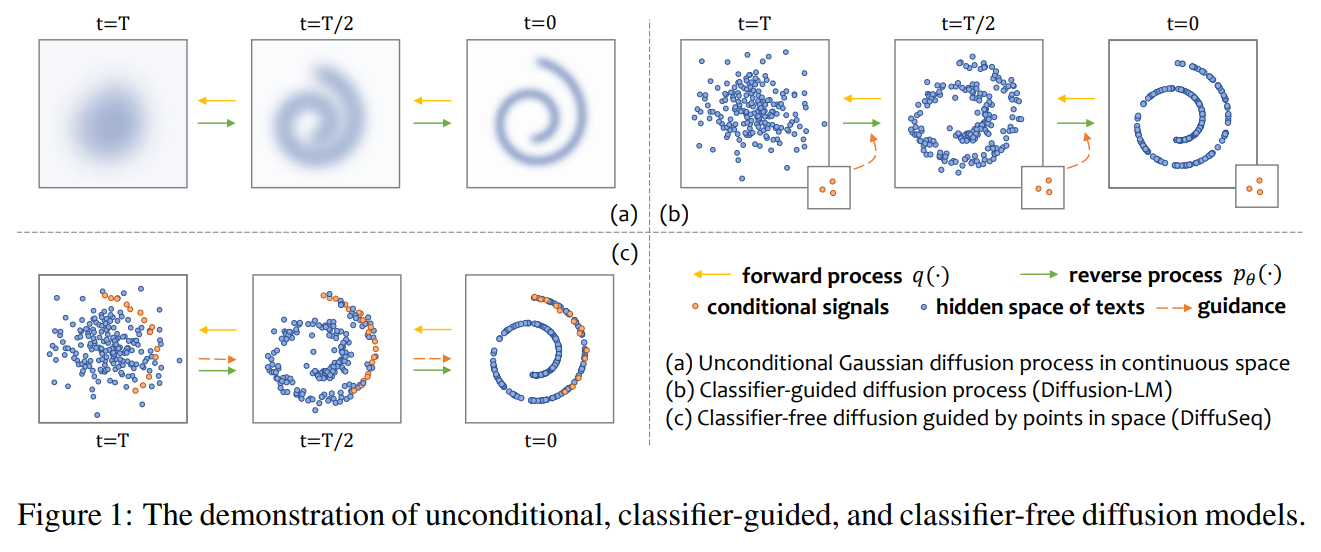
DiffuSeq의 핵심 아이디어는 조건부 생성을 위해 소스 시퀀스는 보존하고 타겟 시퀀스에만 노이즈를 적용하는 것입니다.

1. 임베딩 변환: 먼저 이산적인 텍스트를 연속 공간으로 변환합니다:

   \[\text{EMB}(w^{x\oplus y}) = [\text{EMB}(w_1^x), ..., \text{EMB}(w_m^x), \text{EMB}(w_1^y), ..., \text{EMB}(w_n^y)]\]

   여기서:

   • \(\text{EMB}(\cdot)\) : 텍스트 토큰을 연속적인 벡터로 변환하는 임베딩 함수
   • \(w^{x\oplus y}\) : 소스와 타겟 시퀀스의 결합
   • 결과 차원: \((m+n) \times d\) (각 토큰이 \(d\) 차원 벡터로 변환됨)

2. 부분 노이징 적용: \(z_t = x_t \oplus y_t\) 로 표기할 때, 전방 과정 \(q(z_t|z_{t-1})\) 에서:

   • \(x_t\) (소스 부분): 노이즈 추가 없이 그대로 유지
   • \(y_t\) (타겟 부분): 노이즈 추가

   이 접근법은 조건부(소스)는 유지하면서 생성해야 할 부분(타겟)만 노이즈화하여 조건부 생성을 가능하게 합니다.

3.3 조건부 디노이징(Conditional Denoising)

트랜스포머 아키텍처를 사용한 확산 모델 \(f_\theta(z_t, t)\) 를 통해 \(x_t\) (조건)와 \(y_t\) (생성 대상) 사이의 의미론적 관계를 모델링합니다.

• 특징: 외부 분류기 없이 단일 모델 내에서 조건부 가이드 수행
• 장점: 텍스트-이미지 생성에서처럼 별도의 사전 학습된 모델에 의존하지 않음

3.4 학습 목표: 변분 하한(VLBO)

학습 목표는 변분 하한(Variational Lower Bound, VLBO)을 최소화하는 것입니다:

\[\mathcal{L}_{\text{VLB}} = \mathbb{E}_{q(z_{1:T}|z_0)}\left[\log \frac{q(z_T|z_0)}{p_\theta(z_T)} + \sum_{t=2}^{T}\log \frac{q(z_{t-1}|z_0, z_t)}{p_\theta(z_{t-1}|z_t)} + \log \frac{q_\phi(z_0|w^{x\oplus y})}{p_\theta(z_0|z_1)} - \log p_\theta(w^{x\oplus y}|z_0)\right]\]

이는 다음과 같이 간소화됩니다:

\[\min_\theta \mathcal{L}_{\text{VLB}} = \min_\theta \left[\sum_{t=2}^{T}||y_0 - \tilde{f}_\theta(z_t, t)||^2 + ||\text{EMB}(w^y) - \tilde{f}_\theta(z_1, 1)||^2 + \mathcal{R}(||z_0||^2)\right]\]

여기서:

• \(\tilde{f}_\theta(z_t, t)\) : \(y_0\) 에 해당하는 복원된 \(z_0\) 의 부분
• \(\mathcal{R}(\|z_0\|^2)\) : 임베딩 학습을 정규화하는 항

3.5 중요도 샘플링(Importance Sampling)

학습 효율성을 높이기 위해 모든 확산 단계를 균등하게 샘플링하지 않고, 손실이 큰 단계에 더 많은 자원을 할당합니다:

\[\mathcal{L}_{\text{VLB}} = \mathbb{E}_{t\sim p_t}\left[\frac{L_t}{p_t}\right], \quad p_t \propto \sqrt{\mathbb{E}[L_t^2]}, \quad \sum_{t=0}^{T-1}p_t = 1\]

여기서:

• \(L_t\) : 시간 단계 \(t\)에서의 손실
• \(p_t\) : 시간 단계 \(t\)를 샘플링할 확률
• \(\sqrt{\mathbb{E}[L_t^2]}\) : 시간 단계 \(t\)에서 예상되는 손실의 크기

4. 다양한 생성 모델과의 이론적 연결성

DiffuSeq가 기존 생성 모델과 어떻게 연결되는지 이해하는 것은 중요합니다. 여기서는 세 가지 주요 패러다임과의 관계를 설명합니다.

4.1 자기회귀(AR) 모델

자기회귀 모델은 토큰을 순차적으로(왼쪽에서 오른쪽으로) 생성합니다:

\[p_{\text{AR}}(w_{1:n}^y|w^x) = p(w_1^y|w^x)\prod_{i=1,...,n-1}p(w_{i+1}^y|w_{1:i}^y, w^x)\]

여기서:
\(p(w_1^y|w^x)\) : 첫 번째 토큰의 초기 예측
\(p(w_{i+1}^y|w_{1:i}^y, w^x)\) : 왼쪽 컨텍스트를 기반으로 한 다음 토큰 예측

4.2 완전 비자기회귀(Fully-NAR) 모델

모든 토큰을 독립적으로 병렬 생성합니다:

\[p_{\text{fully-NAR}}(w_{1:n}^y|w^x) = \prod_{i=1,...,n}p(w_i^y|w^x)\]

여기서:
\(p(w_i^y | w^x)\) : 각 출력 토큰이 입력에만 의존하고 다른 출력 토큰과는 독립적

4.3 반복적 비자기회귀(Iterative-NAR) 모델

여러 중간 시퀀스를 통해 출력을 점진적으로 개선합니다:

\[p_{\text{iter-NAR}}(w_{1:n}^y|w^x) = \sum_{w_1^y,...,w_{K-1}^y}\prod_{i=1...n}p(w_{1,i}^y|w^x)\prod_{k=1..K-1}\prod_{i=1...n}p(w_{k+1,i}^y|w_{k,1:n}^y, w^x)\]

여기서:
\(w_1^y,...,w_{K-1}^y\) : \(K-1\) 개의 중간 시퀀스
\(p(w_{1,i}^y|w^x)\) : 초기 예측
\(p(w_{k+1,i}^y|w_{k,1:n}^y, w^x)\) : 전체 컨텍스트를 기반으로 한 점진적 개선

4.4 DiffuSeq 모델

연속적인 공간에서 확산 과정을 통해 생성:

\[p_{\text{diffusion}}(w^y|w^x) = \int_{y_T,...,y_0} p(w^y|y_0, w^x) \prod_{t=T,...,1} p(y_{t-1}|y_t, w^x)\]

연속 공간과 이산 토큰을 연결하는 라운딩 연산을 추가하면:

\[p_{\text{DiffuSeq}}(w^y|w^x) = \sum_{w_T^y,...,w_1^y}\int_{y_T,...,y_0} p(w^y|y_0, w^x)\prod_{t=T,...,1}p(y_{t-1}|w_t^y)p(w_t^y|y_t, w^x)\]

4.5 이론적 연결

논문의 분석에 따르면, DiffuSeq는 반복적 NAR 모델의 확장으로 볼 수 있습니다. 주요 차이점은:

• 반복적 NAR: 이산 토큰 공간에서 작동
• DiffuSeq: 연속 임베딩 공간에서 작동, 더 많은 자유도

이론적으로 DiffuSeq는 AR과 NAR 모델 사이의 “조건부 총 상관관계”(conditional total correlation) 간극을 줄일 수 있습니다.

5. 실험 설계 및 구현 세부사항

5.1 데이터셋

DiffuSeq는 4개의 다양한 시퀀스-투-시퀀스 태스크에서 평가되었습니다:

1. 오픈 도메인 대화: Commonsense Conversation Dataset (300만 대화 쌍)
2. 질문 생성: Quasar-T 데이터셋 (119,000 문서-질문 쌍)
3. 텍스트 단순화: 677,000개의 복잡한-단순 문장 쌍
4. 패러프레이징: QQP 데이터셋 (147,000 긍정 쌍)

5.2 모델 아키텍처 및 하이퍼파라미터

• 기본 구조: 12층 트랜스포머, 12개 어텐션 헤드
• 임베딩 차원: \(d = 128\)
• 확산 단계: \(T = 2,000\)
• 노이즈 스케줄: 제곱근 스케줄 (\(\alpha_t = 1 - \sqrt{t/T + s}\) , \(s\) 는 작은 상수)
• 토크나이저: BPE(Byte Pair Encoding)
• 디코딩 전략: MBR(Minimum Bayes Risk)
• 학습 환경: NVIDIA A100 GPU 4대 (학습), 1대 (추론)

5.3 평가 메트릭

생성된 텍스트는 두 가지 주요 측면에서 평가되었습니다:

품질 메트릭:

• BLEU: n-gram 기반 정밀도 (n=1~4)
• ROUGE-L: 최장 공통 부분 수열 기반 통계
• BERTScore: 의미론적 유사성 측정 (microsoft/deberta-xlarge-mnli 모델 사용)

다양성 메트릭:

• dist-1: 개별 문장 내 유니그램 다양성 (높을수록 반복이 적음)
• self-BLEU: 문장 간 n-gram 중복 (낮을수록 다양성이 높음)
• div-4: 소스 문장당 고유 4-gram 비율 (높을수록 다양성이 높음)

6. 주요 실험 결과 및 분석

6.1 품질 및 다양성 비교

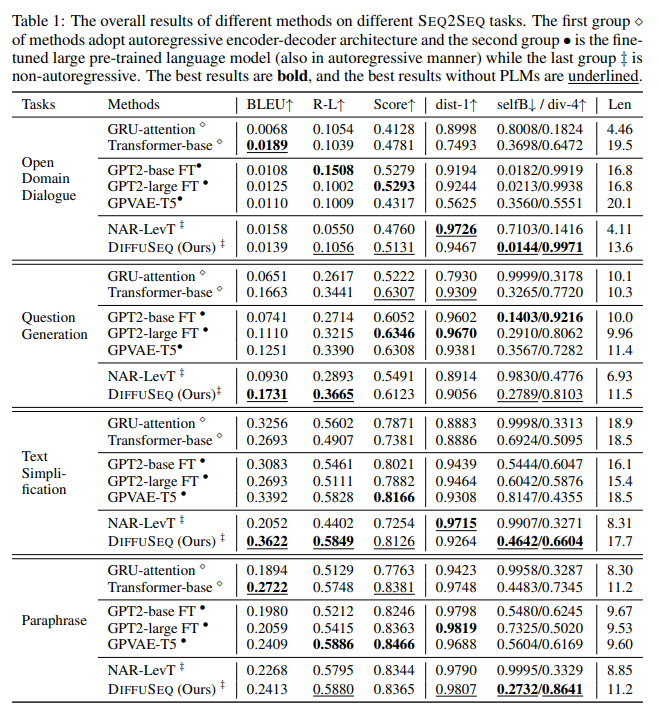
DiffuSeq는 세 가지 주요 비교군과 평가되었습니다:

• 인코더-디코더 모델 (GRU 어텐션, 트랜스포머)
• 사전 학습된 대형 언어 모델 (GPT2-base, GPT2-large, GPVAE-T5)
• 비자기회귀 모델 (NAR-LevT)

주요 발견:

1. 품질: DiffuSeq는 대부분의 태스크에서 비교군과 동등하거나 더 나은 품질 점수를 달성
2. 다양성: DiffuSeq는 특히 문장 수준 다양성(self-BLEU, div-4)에서 자기회귀 모델들을 크게 능가

6.2 품질과 다양성의 트레이드오프

실험 결과, DiffuSeq는 품질과 다양성 사이에서 더 나은 균형을 제공합니다:

• 자기회귀 모델은 일반적으로 높은 품질을 보이지만 제한된 다양성을 가짐
• DiffuSeq는 유사한 품질 수준을 유지하면서 훨씬 더 다양한 출력을 생성

6.3 MBR 디코딩의 효과

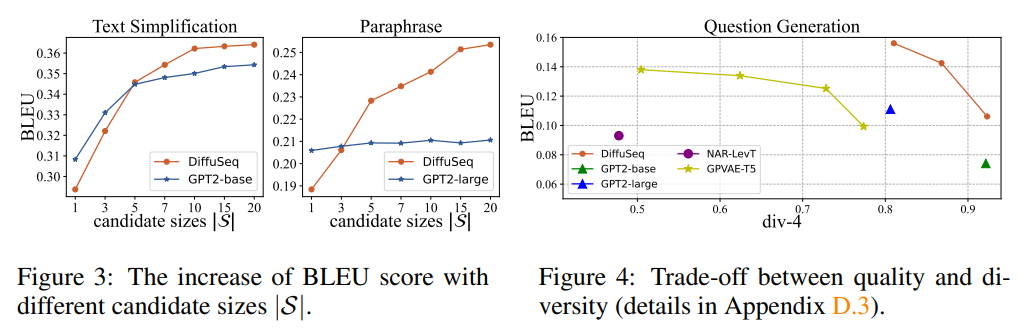
후보 집합 크기(|S|) 의 영향:
작은 |S| (1~3)에서는 DiffuSeq가 GPT2보다 낮은 성능을 보임
|S| 가 증가함에 따라 DiffuSeq는 GPT2를 능가하기 시작
|S|=20 에서도 DiffuSeq는 계속 상승 추세를 보이는 반면, GPT2는 평탄화

이는 DiffuSeq가 생성하는 다양한 후보가 MBR을 통해 더 높은 품질로 이어짐을 시사합니다.

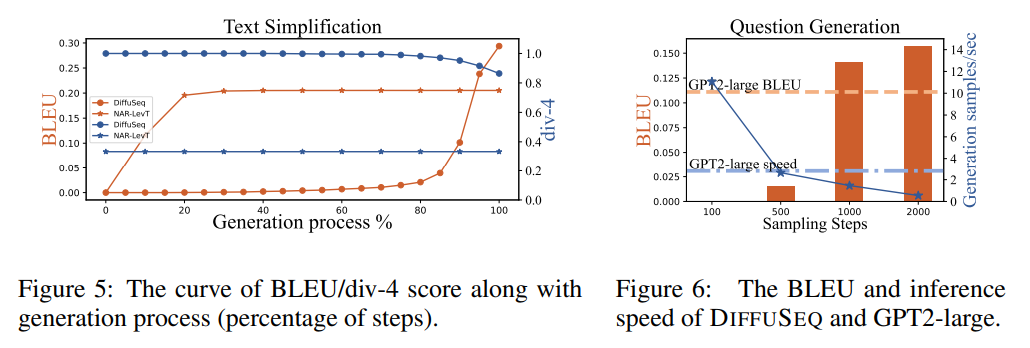
6.4 생성 과정 분석

LevT(반복적 NAR)와 DiffuSeq의 생성 과정 비교:

• LevT: 초기에 품질이 급격히 증가하다가 이후 둔화
• DiffuSeq: 처음에는 품질이 천천히 증가하다가 후반부에 급격히 향상

다양성 측면에서는 두 모델 모두 초기 단계에서 결정되지만, DiffuSeq가 모든 단계에서 일관되게 더 높은 다양성을 보입니다.

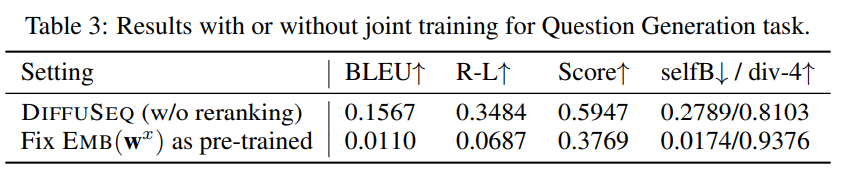
6.5 추론 속도 개선

DDIM(Denoising Diffusion Implicit Models) 기법을 활용한 추론 가속화:

• 확산 단계를 2,000에서 1,000으로 줄여도 GPT2-large보다 높은 BLEU 점수 유지
• 추론 속도도 GPT2-large에 근접 (초당 생성 샘플 수 기준)

6.6 공동 학습의 중요성

소스와 타겟 시퀀스의 임베딩 공유 효과:

• 별도의 사전 학습된 임베딩 사용 시 성능이 크게 저하 (BLEU 0.1567 → 0.0110)
• 이는 DiffuSeq의 공동 학습 접근법의 중요성을 보여줌

7. 결론 및 미래 연구 방향

DiffuSeq는 확산 모델을 시퀀스-투-시퀀스 텍스트 생성에 성공적으로 적용한 첫 시도로서, 다음과 같은 중요한 기여를 했습니다:

1. 시스템적 기여: 확산 모델의 텍스트 적용을 위한 부분 노이징 및 조건부 디노이징 메커니즘 제안

2. 이론적 기여: AR, NAR, 확산 모델 간의 연결성을 명확히 하여 DiffuSeq가 반복적 NAR 모델의 확장임을 증명

3. 실증적 기여: 품질과 다양성이라는 두 가지 핵심 목표를 동시에 달성할 수 있는 새로운 방법론 제시

미래 연구 방향으로는 다음과 같은 가능성이 있습니다:

1. 효율성 개선: 더 빠른 샘플링 알고리즘 개발
2. 사전 학습 접목: 대형 언어 모델의 지식을 활용하는 방안
3. 다양한 NLP 작업 확장: 기계 번역, 요약 등으로의 적용
4. 조절 가능성 강화: 다양한 가이드 메커니즘 통합